21924번: 도시 건설
첫 번째 줄에 건물의 개수 $N$ $(3 \le N \le 10^5 )$와 도로의 개수 $M$ $(2 \le M \le min( {N(N-1) \over 2}, 5×10^5)) $가 주어진다. 두 번째 줄 부터 $M + 1$줄까지 건물의 번호 $a$, $b$ $(1 \le a, b \le N, a ≠ b)$와 두
www.acmicpc.net
문제
채완이는 신도시에 건물 사이를 잇는 양방향 도로를 만들려는 공사 계획을 세웠다.
공사 계획을 검토하면서 비용이 생각보다 많이 드는 것을 확인했다.
채완이는 공사하는 데 드는 비용을 아끼려고 한다.
모든 건물이 도로를 통해 연결되도록 최소한의 도로를 만들려고 한다.
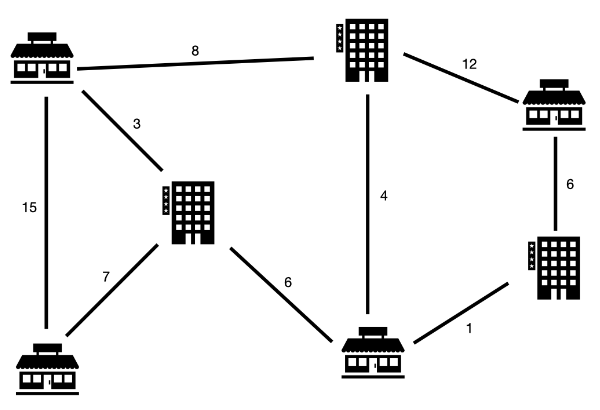
위 그림에서 건물과 직선으로 표시된 도로, 해당 도로를 만들 때 드는 비용을 표시해놓은 지도이다.
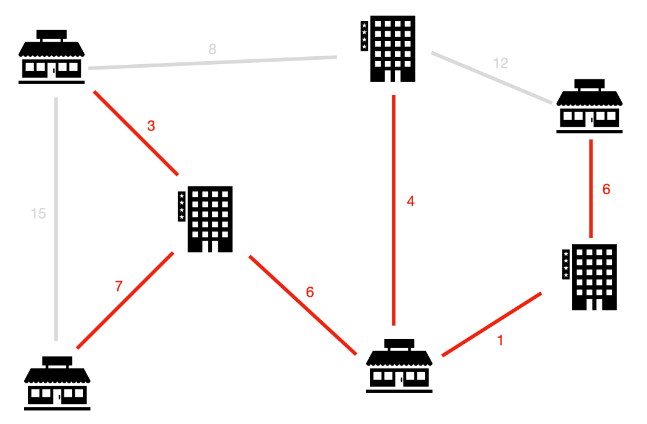
그림에 있는 도로를 다 설치할 때 드는 비용은 62이다. 모든 건물을 연결하는 도로만 만드는 비용은 27로 절약하는 비용은 35이다.
채완이는 도로가 너무 많아 절약되는 금액을 계산하는 데 어려움을 겪고 있다.
채완이를 대신해 얼마나 절약이 되는지 계산해주자.
입력
첫 번째 줄에 건물의 개수 와 도로의 개수 가 주어진다.
두 번째 줄 부터 줄까지 건물의 번호 , 와 두 건물 사이 도로를 만들 때 드는 비용 가 주어진다. 같은 쌍의 건물을 연결하는 두 도로는 주어지지 않는다.
출력
예산을 얼마나 절약 할 수 있는지 출력한다. 만약 모든 건물이 연결되어 있지 않는다면 -1을 출력한다.
코드
import sys
input = sys.stdin.readline
from heapq import heappop, heappush
n, m = map(int, input().split())
parent = [i for i in range(n+1)]
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]
def union(a, b):
a = find(a)
b = find(b)
if a == b:
return
if a < b:
parent[b] = a
else:
parent[a] = b
roads = []
total_cost = 0
for _ in range(m):
a, b, c = map(int, input().split())
heappush(roads, (c, a, b))
total_cost += c
min_cost, cnt = 0, 1
while roads:
c, a, b = heappop(roads)
if find(a) != find(b): # 사이클 형성하는지 체크
union(a,b)
min_cost += c
cnt += 1
if cnt == n: # 모든 건물 연결 완료
print(total_cost-min_cost)
exit()
print(-1)최소 가중치를 갖는 그래프를 만들어야 하는 문제이므로 MST를 만들어주면 된다.
크루스칼 알고리즘을 이용하여 사이클을 형성하지 않으며 매번 최소 가중치를 갖는 간선을 선택하여 MST를 만들었다.
'문제풀이 > MST' 카테고리의 다른 글
| [Python/파이썬] 백준 14621번 나만 안되는 연애 (0) | 2023.04.07 |
|---|---|
| [Python/파이썬] 백준 1774번 우주신과의 교감 (0) | 2023.04.07 |
| [Python/파이썬] 백준 16398번 행성 연결 (0) | 2023.04.06 |
| [Python/파이썬] 백준 1647번 도시 분할 계획 (0) | 2023.04.06 |
| [Python/파이썬] 백준 1922번 네트워크 연결 (0) | 2023.04.06 |
