10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net
문제
수 N개 $A_1, A_2, ..., A_N$이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오.
즉, $A_i + ... + A_j$ (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j) 쌍의 개수를 구해야 한다.
입력
첫째 줄에 N과 M이 주어진다. (1 ≤ N ≤ $10^6$, 2 ≤ M ≤ $10^3$)
둘째 줄에 N개의 수 $A_1, A_2, ..., A_N$이 주어진다. (0 ≤ $A_i$ ≤ $109$)
출력
첫째 줄에 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 출력한다.
코드
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
arr = list(map(int, input().split()))
pfSum = 0
mod_lst = [0] * m
for i in range(n):
pfSum += arr[i]
mod_lst[pfSum % m] += 1
ans = 0
for i in mod_lst:
ans += i * (i-1) // 2
print(ans + mod_lst[0])누적합을 이용하여야 하는 문제인건 대충 알겠는데 어떻게 풀지 감이 안 와서 결국 구글링해서 참조해서 풀었다
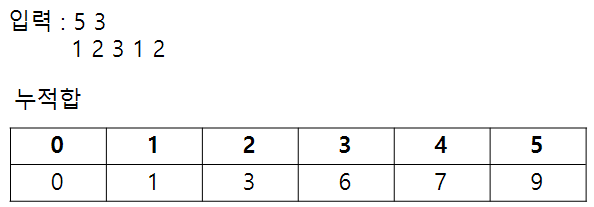
입력이 문제의 예제1과 같을때 이 배열의 누적합은 위의 표와 같이 나온다. 풀이에서는 굳이 저장할 필요가 없어서 따로 저장하지는 않았다. pfSum에 매번 누적합을 저장하고 이 값을 m으로 나눈다. 이 값이 pfSum % m인데 이 값 역시도 풀이에서는 인덱스마다 어떤 값인지 굳이 저장할 필요가 없어서 저장하지는 않았지만 보기 쉽게 표로 정리하여 살펴보면 다음과 같다. 입력으로 받은 배열(arr)의 인덱스를 1부터 시작한다고 생각하고 보면 된다.

pfSum % m의 개수만 필요하기 때문에 mod_lst에 pfSum % m 값별로 개수를 넣었다.
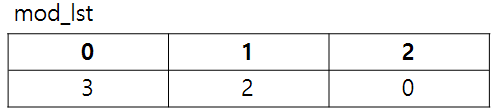
$A_i + ... + A_j$ (i ≤ j) 의 합이 M으로 나누어 떨어지려면 $A_i + ... + A_j$ (i ≤ j) 의 합을 M으로 나눈 나머지 값이 같은 값끼리 빼면 된다. 그러므로 mod_lst에서 각 나머지 값별로 순서에 상관없이 다른 2개의 값을 뽑는 경우의 수들을 구하여 그 합을 구하면 된다. n개 중 2개를 뽑는 경우의 수는 다음과 같다.
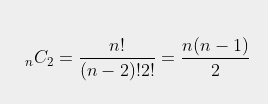
그리고 나머지가 0일 때의 값을 한 번 더해주는데 이것은 나머지가 0인 값들은 굳이 2개를 뽑지 않아도 m으로 나누어 떨어지기 때문이다.
'문제풀이 > 누적합' 카테고리의 다른 글
| [Python/파이썬] 백준 16139번 인간-컴퓨터 상호작용 (0) | 2023.07.25 |
|---|---|
| [Python/파이썬] 백준 20440번 🎵니가 싫어 싫어 너무 싫어 싫어 오지 마 내게 찝쩍대지마🎵 - 1 (0) | 2023.07.04 |
| [Python/파이썬] 백준 21758번 꿀 따기 (0) | 2023.05.24 |
| [Python/파이썬] 백준 1749번 점수따먹기 (0) | 2023.05.12 |
| [Python/파이썬] 백준 2015번 수들의 합 4 (0) | 2023.05.10 |
10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net
문제
수 N개 $A_1, A_2, ..., A_N$이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오.
즉, $A_i + ... + A_j$ (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j) 쌍의 개수를 구해야 한다.
입력
첫째 줄에 N과 M이 주어진다. (1 ≤ N ≤ $10^6$, 2 ≤ M ≤ $10^3$)
둘째 줄에 N개의 수 $A_1, A_2, ..., A_N$이 주어진다. (0 ≤ $A_i$ ≤ $109$)
출력
첫째 줄에 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 출력한다.
코드
import sys input = sys.stdin.readline n, m = map(int, input().split()) arr = list(map(int, input().split())) pfSum = 0 mod_lst = [0] * m for i in range(n): pfSum += arr[i] mod_lst[pfSum % m] += 1 ans = 0 for i in mod_lst: ans += i * (i-1) // 2 print(ans + mod_lst[0])
누적합을 이용하여야 하는 문제인건 대충 알겠는데 어떻게 풀지 감이 안 와서 결국 구글링해서 참조해서 풀었다

입력이 문제의 예제1과 같을때 이 배열의 누적합은 위의 표와 같이 나온다. 풀이에서는 굳이 저장할 필요가 없어서 따로 저장하지는 않았다. pfSum에 매번 누적합을 저장하고 이 값을 m으로 나눈다. 이 값이 pfSum % m인데 이 값 역시도 풀이에서는 인덱스마다 어떤 값인지 굳이 저장할 필요가 없어서 저장하지는 않았지만 보기 쉽게 표로 정리하여 살펴보면 다음과 같다. 입력으로 받은 배열(arr)의 인덱스를 1부터 시작한다고 생각하고 보면 된다.

pfSum % m의 개수만 필요하기 때문에 mod_lst에 pfSum % m 값별로 개수를 넣었다.

$A_i + ... + A_j$ (i ≤ j) 의 합이 M으로 나누어 떨어지려면 $A_i + ... + A_j$ (i ≤ j) 의 합을 M으로 나눈 나머지 값이 같은 값끼리 빼면 된다. 그러므로 mod_lst에서 각 나머지 값별로 순서에 상관없이 다른 2개의 값을 뽑는 경우의 수들을 구하여 그 합을 구하면 된다. n개 중 2개를 뽑는 경우의 수는 다음과 같다.
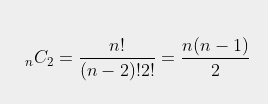
그리고 나머지가 0일 때의 값을 한 번 더해주는데 이것은 나머지가 0인 값들은 굳이 2개를 뽑지 않아도 m으로 나누어 떨어지기 때문이다.
'문제풀이 > 누적합' 카테고리의 다른 글
| [Python/파이썬] 백준 16139번 인간-컴퓨터 상호작용 (0) | 2023.07.25 |
|---|---|
| [Python/파이썬] 백준 20440번 🎵니가 싫어 싫어 너무 싫어 싫어 오지 마 내게 찝쩍대지마🎵 - 1 (0) | 2023.07.04 |
| [Python/파이썬] 백준 21758번 꿀 따기 (0) | 2023.05.24 |
| [Python/파이썬] 백준 1749번 점수따먹기 (0) | 2023.05.12 |
| [Python/파이썬] 백준 2015번 수들의 합 4 (0) | 2023.05.10 |
